
Было проведено бесчисленное множество научных проверок общей теории относительности Эйнштейна, подвергнув эту идею самым строгим ограничениям, когда-либо полученным человечеством. Первое решение Эйнштейна касалось предела слабого поля вокруг одной массы.
Автор: Итан Сигел
- Уравнения поля Эйнштейна кажутся очень простыми, но в них заложена огромная сложность.
- То, что выглядит как одно компактное уравнение, на самом деле представляет собой 16 сложных уравнений, связывающих кривизну пространства-времени с материей и энергией во Вселенной.
- Это показывает, что гравитация принципиально отличается от всех других сил, и тем не менее, во многих отношениях это единственное, что мы можем понять.
Хотя Эйнштейн является легендарной фигурой в науке по целому ряду причин — E = mc², фотоэлектрический эффект и представление о том, что скорость света постоянна для всех, — его самое устойчивое открытие также является наименее понятым: его теория гравитации, общая теория относительности. До Эйнштейна мы думали о гравитации в ньютоновских терминах: что все во Вселенной, имеющее массу, мгновенно притягивает любую другую массу в зависимости от значения их масс, гравитационной постоянной и квадрата расстояния между ними. Но концепция Эйнштейна была совершенно иной, основанной на идее, что пространство и время были объединены в ткань, пространство-время, и что кривизна пространства-времени говорила не только материи, но и энергии, как двигаться в нем.
Эта фундаментальная идея — что материя и энергия говорят пространству-времени, как искривляться, и что искривленное пространство-время, в свою очередь, говорит материи и энергии, как двигаться, — представляла собой революционно новый взгляд на вселенную. Выдвинутая в 1915 году Эйнштейном и подтвержденная четыре года спустя во время полного солнечного затмения — когда искривление звездного света, исходящего от источников света за солнцем, совпало с предсказаниями Эйнштейна, а не Ньютона, — общая теория относительности прошла все наблюдательные и экспериментальные проверки, которые мы когда-либо придумывали. Тем не менее, несмотря на ее успех на протяжении более 100 лет, почти никто не понимает, что на самом деле представляет собой одно уравнение, управляющее общей теорией относительности. Вот, на простом английском, что оно на самом деле означает.

Исходное уравнение Эйнштейна связывает кривизну пространства-времени с энергией-напряжением системы (вверху). Можно добавить космологический постоянный член (в середине) или, что эквивалентно, его можно сформулировать как темную энергию (внизу), другую форму плотности энергии, вносящую вклад в тензор энергии-напряжения.Кредит: © 2014 Токийский университет; Kavli IPMU
Это уравнение выглядит довольно простым, поскольку в нем присутствует всего несколько символов. Но оно довольно сложное.
- Первый из них, G μν , известен как тензор Эйнштейна и представляет кривизну пространства.
- Вторая, Λ, — космологическая постоянная: количество энергии, положительной или отрицательной, присущей самой ткани пространства.
- Третий член, g μν , известен как метрика, которая математически кодирует свойства каждой точки пространства-времени.
- Четвертый член, 8πG/c 4 , является просто произведением констант и известен как гравитационная постоянная Эйнштейна, аналог гравитационной постоянной Ньютона (G), с которой большинство из нас более знакомо.
- Пятый член, T μν , известен как тензор энергии-импульса и описывает локальную (в ближайшей окрестности) энергию, импульс и напряжение в этом пространстве-времени.
Эти пять терминов, связанных друг с другом посредством того, что мы называем уравнениями поля Эйнштейна, достаточны для того, чтобы связать геометрию пространства-времени со всей материей и энергией в нем: отличительная черта общей теории относительности.

Фреска с уравнениями поля Эйнштейна с иллюстрацией преломления света вокруг затменного солнца — наблюдения, которые впервые подтвердили общую теорию относительности еще в 1919 году. Слева показан тензор Эйнштейна, разложенный на тензор Риччи и скаляр Риччи.Фото: Высоцкий / Wikimedia Commons
Вы можете задаться вопросом, что со всеми этими индексами — этими странными комбинациями греческих букв «μν», которые вы видите внизу тензора Эйнштейна, метрики и тензора энергии-импульса. Чаще всего, когда мы записываем уравнение, мы записываем скалярное уравнение, то есть уравнение, которое представляет собой только одно равенство, где сумма всего в левой части равна всему в правой. Но мы также можем записать системы уравнений и представить их с помощью одной простой формулировки, которая кодирует эти отношения.
E = mc² — скалярное уравнение, поскольку энергия (E), масса (m) и скорость света (c) имеют только отдельные уникальные значения. Но ньютоновское F = m a — это не одно уравнение, а три отдельных уравнения: F x = ma x для направления «x», F y = ma y для направления «y» и F z = ma z для направления «z». В общей теории относительности тот факт, что у нас есть четыре измерения (три пространственных и одно временное), а также два нижних индекса, которые физики называют индексами, означает, что нет одного уравнения, и даже не три или четыре. Вместо этого у нас есть каждое из четырех измерений (t, x, y, z), влияющее на каждое из четырех других (t, x, y, z), что в общей сложности составляет 4 × 4, или 16, уравнений.

Вместо пустой, пустой, трехмерной сетки, размещение массы приводит к тому, что то, что было бы «прямыми» линиями, становится искривленным на определенную величину. В общей теории относительности пространство и время непрерывны, и все формы энергии вносят вклад в искривление пространства-времени.Автор: Кристофер Витале из Networkologies и Института Пратта
Зачем нам нужно так много уравнений только для описания гравитации, тогда как Ньютону было достаточно одного?
Потому что геометрия — сложный зверь, потому что мы работаем в четырех измерениях, и потому что то, что происходит в одном измерении или даже в одном месте, может распространяться наружу и влиять на каждое место во вселенной, если только вы позволите пройти достаточно времени. Наша вселенная с тремя пространственными измерениями и одним временным измерением означает, что геометрию нашей вселенной можно математически рассматривать как четырехмерное многообразие.
В римановой геометрии, где многообразия не обязаны быть прямыми и жесткими, а могут быть произвольно изогнуты, вы можете разбить эту кривизну на две части: части, которые искажают объем объекта, и части, которые искажают форму объекта. Часть «Риччи» искажает объем и играет роль в тензоре Эйнштейна, поскольку тензор Эйнштейна состоит из тензора Риччи и скаляра Риччи с некоторыми константами и добавленной метрикой. Часть «Вейля» искажает форму и, как ни странно, не играет никакой роли в уравнениях поля Эйнштейна.
Уравнения поля Эйнштейна — это не просто одно уравнение, а скорее набор из 16 различных уравнений: по одному для каждой комбинации «4 × 4». Когда один компонент или аспект вселенной изменяется, например, пространственная кривизна в любой точке или в любом направлении, любой другой компонент также может измениться в ответ. Эта структура во многих отношениях выводит концепцию дифференциального уравнения на новый уровень.
Дифференциальное уравнение — это любое уравнение, в котором можно выполнить следующие действия:
- вы можете указать начальные условия вашей системы, например, что присутствует, где и когда это находится, и как это движется,
- затем вы можете включить эти условия в ваше дифференциальное уравнение,
- и уравнение покажет вам, как эти вещи развиваются во времени, переходя к следующему моменту,
- где вы можете включить эту информацию обратно в дифференциальное уравнение, которое затем скажет вам, что произойдет далее, в следующее мгновение.
Это чрезвычайно мощная структура, и именно по этой причине Ньютону потребовалось изобрести исчисление, чтобы такие вещи, как движение и гравитация, стали понятными научными областями.

Когда вы помещаете даже одну точечную массу в пространство-время, вы в результате искривляете ткань пространства-времени повсюду. Уравнения поля Эйнштейна позволяют вам связать кривизну пространства-времени с материей и энергией, в принципе, для любого выбранного вами распределения. Кредит: Джонсон Мартин / Pixabay
Только когда мы начинаем иметь дело с общей теорией относительности, это не просто одно уравнение или даже ряд независимых уравнений, которые все распространяются и развиваются в своем собственном измерении. Вместо этого, поскольку то, что происходит в одном направлении или измерении, влияет на все остальные, у нас есть 16 связанных, взаимозависимых уравнений, и по мере того, как объекты движутся и ускоряются в пространстве-времени, изменяется энергия-напряжение, а также пространственная кривизна.
Однако эти «16 уравнений» не совсем уникальны! Во-первых, тензор Эйнштейна симметричен, что означает, что между каждым компонентом существует связь, которая связывает одно направление с другим. В частности, если ваши четыре координаты для времени и пространства — это (t, x, y, z), то:
- компонент «tx» будет эквивалентен компоненту «xt»,
- компонент «ty» будет эквивалентен компоненту «yt»,
- компонент «tz» будет эквивалентен компоненту «zt»,
- компонент «yx» будет эквивалентен компоненту «xy»,
- компонент «zx» будет эквивалентен компоненту «xz»,
- а компонент «zy» будет эквивалентен компоненту «yz».
Внезапно оказалось, что уникальных уравнений не 16, а всего 10.
Кроме того, есть четыре соотношения, которые связывают кривизну этих различных измерений вместе: тождества Бьянки. Из 10 оставшихся уникальных уравнений только шесть являются независимыми, поскольку эти четыре соотношения еще больше снижают общее число независимых переменных. Сила этой части дает нам свободу выбора любой системы координат, которая нам нравится, что буквально является силой относительности: каждый наблюдатель, независимо от его положения или движения, видит одни и те же законы физики, такие как одни и те же правила общей теории относительности.
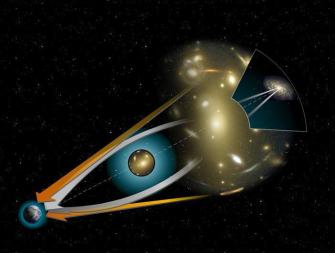
Иллюстрация гравитационного линзирования и искривления звездного света из-за массы. Искривление пространства может быть настолько сильным, что свет может следовать по нескольким путям из одной точки в другую.Кредит: NASA / STScI
Есть и другие свойства этого набора уравнений, которые чрезвычайно важны. В частности, если вы возьмете дивергенцию тензора энергии-импульса, вы всегда, всегда получите ноль, не только в целом, но и для каждого отдельного компонента. Это означает, что у вас есть четыре симметрии: нет дивергенции во временном измерении или любом из пространственных измерений, и каждый раз, когда у вас есть симметрия в физике, у вас также есть сохраняющаяся величина.
В общей теории относительности эти сохраняющиеся величины преобразуются в энергию (для измерения времени), а также в импульс в направлениях x, y и z (для пространственных измерений). Точно так же, по крайней мере локально в вашем ближайшем окружении, и энергия, и импульс сохраняются для отдельных систем. Несмотря на то, что в общей теории относительности невозможно определить такие вещи, как «глобальная энергия», для любой локальной системы в рамках общей теории относительности и энергия, и импульс сохраняются всегда; это требование теории.

Когда массы движутся в пространстве-времени относительно друг друга, они вызывают излучение гравитационных волн: рябь через ткань самого пространства. Эта рябь математически закодирована в метрическом тензоре.Кредит: ESO / Л. Кальсада
Другое свойство общей теории относительности, которое отличается от большинства других физических теорий, заключается в том, что общая теория относительности как теория нелинейна. Если у вас есть решение для вашей теории, например, «каковы свойства пространства-времени, когда я кладу одну точечную массу», у вас возникнет соблазн сделать утверждение вроде: «Если я положу две точечные массы, то я могу объединить решение для массы № 1 и массы № 2 и получить другое решение: решение для обеих масс вместе».
Это верно, но только если у вас линейная теория. Ньютоновская гравитация — это линейная теория: гравитационное поле — это гравитационное поле каждого объекта, сложенное вместе и наложенное друг на друга. Электромагнетизм Максвелла похож: электромагнитное поле двух зарядов, двух токов или заряда и тока можно вычислить по отдельности и сложить вместе, чтобы получить чистое электромагнитное поле. Это верно даже в квантовой механике, поскольку уравнение Шредингера также линейно (по волновой функции).
Но уравнения Эйнштейна нелинейны, что означает, что вы не можете этого сделать. Если вы знаете кривизну пространства-времени для одной точечной массы, а затем вы кладете вторую точечную массу и спрашиваете: «Как пространство-время искривлено сейчас?», мы не можем записать точное решение. Фактически, даже сегодня, более чем через 100 лет после того, как общая теория относительности была впервые выдвинута, в теории относительности все еще известно всего около ~20 точных решений, и пространство-время с двумя точечными массами в нем все еще не является одним из них.

Фотография Итана Сигела на гиперстене Американского астрономического общества в 2017 году вместе с первым уравнением Фридмана справа — которое иногда называют самым важным уравнением во Вселенной и одним из редких точных решений в общей теории относительности.Кредит: Харли Тронсон / Институт Периметра)
Первоначально Эйнштейн сформулировал общую теорию относительности только с первым и последним членами уравнений, то есть с тензором Эйнштейна с одной стороны и тензором энергии-импульса (умноженным на гравитационную постоянную Эйнштейна) с другой стороны. Он добавил только космологическую постоянную, по крайней мере, согласно легенде, потому что не мог переварить последствия вселенной, которая была вынуждена либо расширяться, либо сжиматься.
И все же, сама космологическая константа была бы революционным дополнением, даже если бы оказалось, что природа не имеет ненулевой константы (в форме сегодняшней темной энергии) по простой, но увлекательной причине. Космологическая константа, математически, является буквально единственной «дополнительной» вещью, которую вы можете добавить в общую теорию относительности, не меняя принципиально природу взаимосвязи между материей и энергией и кривизной пространства-времени.
Однако сердце общей теории относительности — это не космологическая постоянная, которая является просто одним конкретным типом «энергии», которую вы можете добавить, а два других более общих термина. Тензор Эйнштейна, G μν , говорит нам, какова кривизна пространства, и он связан с тензором энергии-импульса, T μν , который говорит нам, как распределены материя и энергия во Вселенной.

Квантовая гравитация пытается объединить Общую теорию относительности Эйнштейна с квантовой механикой. Квантовые поправки к классической гравитации визуализируются в виде петлевых диаграмм, как показано здесь белым цветом.Кредит: Национальная ускорительная лаборатория SLAC
В нашей Вселенной мы почти всегда делаем приближения. Если бы мы проигнорировали 15 из 16 уравнений Эйнштейна и просто сохранили компонент «энергия», вы бы восстановили теорию, которую он заменил: закон тяготения Ньютона. Если бы вы вместо этого сделали Вселенную симметричной во всех пространственных измерениях и не позволили ей вращаться, вы получили бы изотропную и однородную Вселенную, управляемую уравнениями Фридмана (и, следовательно, обязанную расширяться или сжиматься). В самых больших космических масштабах это, по-видимому, на самом деле описывает Вселенную, в которой мы живем.
Но вы также можете ввести любое распределение материи и энергии, а также любую совокупность полей и частиц, которая вам нравится, и если вы сможете это записать, уравнения Эйнштейна свяжут геометрию вашего пространства-времени с тем, как искривлена сама Вселенная, с тензором энергии-импульса, который представляет собой распределение энергии, импульса и напряжения.
Если на самом деле существует «теория всего», описывающая как гравитацию, так и квантовую вселенную, то необходимо будет рассмотреть фундаментальные различия между этими концепциями, включая принципиально нелинейную природу теории Эйнштейна. В настоящее время, учитывая их чрезвычайно разные свойства, объединение гравитации с другими квантовыми силами остается одной из самых амбициозных мечтаний во всей теоретической физике.