Ингрид Фаделли , Phys.org
Схема распределения размеров операторов для нескольких классов открытой многочастичной квантовой динамики. Распределение операторов по размерам количественно определяет, как информация скремблируется, и формирует основу нашей структуры для понимания того, как ошибки распространяются в открытой динамике многих тел. Источник: Physical Review Letters (2023). DOI: 10.1103/PhysRevLett.131.160402 — https://phys.org/news/2023-11-universal-framework-scrambling-quantum.html?utm_source=nwletter&utm_medium=email&utm_campaign=daily-nwletter
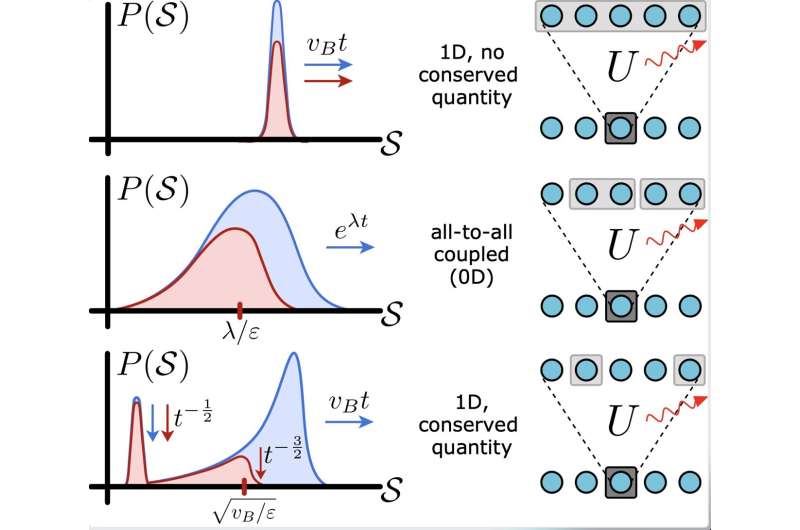
В последние годы физики пытались лучше понять, как квантовая информация распространяется в системах взаимодействующих частиц — явление, часто называемое «скремблированием». Скремблирование в замкнутых системах, физических системах, которые могут обмениваться энергией только со степенями свободы внутри системы, является характерной чертой хаотической квантовой динамики многих тел.
В открытых системах, которые могут обмениваться как энергией, так и веществом со своим окружением, на скремблирование влияют различные дополнительные факторы, включая шум и ошибки. Хотя последствия этих дополнительных воздействий хорошо документированы, приводя, например, к декогеренции, то, как они влияют на скремблирование, остается плохо изученным.
Два исследователя из Калифорнийского университета в Беркли (UC Berkeley) и Гарвардского университета недавно представили новую структуру, опубликованную в Physical Review Letters, которая дает универсальную картину того, как происходит скремблирование информации в открытых квантовых системах. Их структура предлагает особенно простую точку зрения на то, как понять и смоделировать распространение ошибок в открытой квантовой системе, и уже может помочь объяснить некоторые ранее вызывавшие недоумение наблюдения, собранные в экспериментах по магнитному резонансу.
«Норм и я ранее вместе работали над несколькими проектами, посвященными квантовому скремблированию информации», — сказал Томас Шустер, один из исследователей, проводивших исследование, Phys.org.
«Некоторые из наших работ были сосредоточены на том, как измерить скремблирование, а другие — на том, для чего скремблирование может быть полезно. Во всех этих проектах постоянно возникал естественный вопрос: как скремблирование модифицируется ошибками (то есть динамикой «открытой системы»), которые неизбежно возникают в реальных экспериментах? Хотя этот вопрос был явно важен, у нас не было удовлетворительной структуры для ответа на него.»
Изучая этот вопрос, Шустер и Яо поняли, что было бы полезно рассмотреть вещи с экспериментальной точки зрения. В конечном итоге это привело к их недавнему исследованию.
«В динамике открытых систем ошибки возмущают систему, и мы хотели бы знать чувствительность нашего эксперимента к этим возмущениям», — сказал Шустер. «Это говорит о том, что чувствительность эксперимента к ошибкам должна быть связана с тем, как шифруется информация. Основываясь на этой первоначальной идее, мы работали над тем, чтобы точно установить связь между ошибками и скремблированием и проанализировать ее последствия для представляющих интерес физических систем и экспериментов».
Ключевая идея недавнего исследования Шустера и Яо заключается в том, что скремблирование информации в открытой системе в некоторой степени не зависит от микроскопической природы самих ошибок. Скорее всего, все зависит от того, как эти ошибки влияют на так называемое «распределение операторов по размерам», характеризующее сложность оператора с течением времени.
«Динамика распределения операторов по размеру определяет, как именно распространяются ошибки», — объяснил Шустер. «На самом простом уровне это принимает форму двух связанных дифференциальных уравнений. Входными данными для уравнений является то, как изменяется распределение размеров операторов, в то время как выходные данные можно рассматривать как точный прогноз распространения ошибок.»
В то время как некоторые предыдущие исследования намекали на эту связь, никто до сих пор не сформулировал ее ясно и точно. При этом Шустер и Яо обнаружили, что взаимодействие между ошибками и скремблированием было гораздо более тонким, чем предполагалось ранее.
«Еще одним новым результатом нашей работы является то, что ошибки также изменяют поведение самого скремблирования информации», — сказал Шустер. «Это приводит к интересному взаимодействию между ошибками и скремблированием, описываемому уравнениями, упомянутыми выше. Результат этого взаимодействия зависит от природы самой динамики и может быть использован в качестве внутренней характеристики этой динамики в дополнение к прогнозированию различных свойств экспериментов».
Особенно плодотворные условия для применения концепции Шустера и Яо возникают в определенных экспериментах, которые включают так называемую «эргодическую» динамику многих тел. Это может быть осуществлено и подтверждено в будущих работах.
«Приятный сюрприз, который мы обнаружили, когда завершали наши результаты, заключается в том, что наша структура также применима к большому классу экспериментов, называемых «эхо Лошмидта», которые уже несколько десятилетий представляют интерес для сообществ, занимающихся ядерным магнитным резонансом (ЯМР) и квантовым хаосом», — сказал Шустер. «Эхо Лошмидта — это давний мысленный эксперимент в области термодинамики, восходящий к Йозефу Лошмидту и основанию термодинамики в 1800-х годах».
В то время как экспериментальные методы, связанные с эхо Лошмидта, продолжали совершенствоваться, как в экспериментах по квантовому моделированию, так и в исследованиях твердотельного магнитного резонанса, интерпретация этих сигналов, особенно для взаимодействующих гамильтонианов в последнем контексте, по-прежнему оставалась сложной задачей.
«Экспериментаторы применяли различные функциональные формы (например, гауссианы, экспоненты или сигмоиды) к своим данным, но никогда не получали объяснения, почему конкретный эксперимент следовал одной функциональной форме, а не другой», — сказал Шустер. «В начале 2000-х годов исследователи обнаружили структуру для описания эхо Лошмидта в квантовых системах с несколькими телами; однако случай систем со многими телами оставался открытым вопросом. Мы считаем, что наша структура может дать ответ на этот вопрос».
В дополнение к тому, что недавняя работа проливает свет на то, как распространяются ошибки в открытых квантовых системах с множеством тел, она также предполагает, что данные эхо-экспериментов Лошмидта могут содержать больше информации, чем первоначально кажется на первый взгляд.
«Взаимодействие ошибок и динамики распределения операторов по размерам определяет функциональную форму эхо-сигнала Лошмидта», — сказал Шустер. «Мы уверены, что это имеет место в игрушечных моделях, которые мы можем численно изучить, и в будущей работе мы надеемся предоставить более детальный анализ экспериментальных данных Loschmidt echo, чтобы подтвердить, что наша концепция применима и там. Есть несколько признаков, которые убедительно указывают на то, что это так, и я нахожу это весьма захватывающим».
Забегая вперед, Шустер и Яо заинтересованы в применении своей новой структуры к множеству других экспериментов. Они также планируют изучить последствия своих результатов для классического моделирования открытых квантовых систем.
«Нам интересно, может ли наше понимание распространения информации в этих открытых системах на самом деле дать представление о том, сколько квантовых преимуществ можно извлечь из них», — говорит Яо. «И, с другой стороны, можно ли затем разработать новые алгоритмы для эффективного моделирования открытых квантовых систем».
Дополнительная информация: Томас Шустер и др., Рост операторов в открытых квантовых системах, Physical Review Letters (2023). DOI: 10.1103/PhysRevLett.131.160402
Информация о журнале: Physical Review Letters
© 2023 Science X Network